Word-to-Vector Embeddings

One of the biggest, if not THE biggest use cases for artificial intelligence is to mimic our language. This has been acheived to a very high extent by current state-of-the-art models like chatGPT and llama. Although these models have different architectures, knowing intuitively how these models learn to interepret language through much simpler and rudimentary models can pave the way onto learning the current most powerful ones. Before learning about said models, we must explore how exactly these models embed words, or, create internal representations of words which have some latent meaning.

Natural Language Processing

One of the first challenges we face when dealing with language is how do we even deal with words ? Essentially, models are simply statistical techniques or algorithms, which deal with high-dimensional numerical data. The study of language has always been far removed from the study of mathematics. But in this case, our input data is language, or words itself. We must therefore find a way to represent words through numbers, and proceed to work with them. One such way is through what we call word embeddings(more on this later). We represent words through what we might as well call word vectors. But how do we determine what vectors at all to use ? That task is what our model must learn: representing words through vectors. The next question to answer is: what will the model learn exactly ? We can’t induce it to learn the meaning of every word, as that task is beyond our current technology. What we can do, is use clever techniques to induce it to learn some meaning, of certain words. We use models for the purpose of predictions. If we utilize that fact cleverly, we can make the model learn correlation between certain words (our input) to certain meanings (true values). Therefore, for the purpose of this essay, we will define our goal, and see what our model learns.

Defining the task

The best way to understand NLP or RNNs is to make a model and go through the entire process (mathmatically). To begin, we need data. Since we have learning language as our main goal, we do have an infinite amount, but lets focus on a much narrower goal. Given a sentence, our model must predict if that sentence is positive, negative or neutral. Seems complicated ? It’s really not. This particular problem is known as sentiment analysis, and is one of the first problems any beginner deep learning engineer must learn. Before we even begin defining our model through maths, we must define and preprocess our data, so we have numbers instead of words.

Word Embeddings

Ok. Now we have a bunch of sentences. Each sentence is either positive (1), negative (-1) or neutral(0), in it’s sentiment. How do we proceed ? To begin, encode every sentence in a vector. The most simplest form of encoding is simply to create a word index dictionary, where each and every word is associated with an index number, and we simply create a vector with the indexes of the words in the sentence. Here’s an example below:

\begin{array}{l} W o r d i n d e x s \\ I = 1, a = 2, c a t = 3, d o g = 4, h u m a n = 5, a m = 6 \\ S e n t e n c e : I a m a h u m a n \\ V e c t o r e n c o d i n g : [\begin{array}{cccc} 1 & 6 & 2 & 5 \end{array}] \\ S e n t e n c e : I a m a d o g \\ V e c t o r e n c o d i n g : [\begin{array}{cccc} 1 & 6 & 2 & 4 \end{array}] \end{array}

This is indeed a very easy and simple way to encode our sentences and turn them into vectors. Notice, that the sequence of the sentences are preserved, as the model must learn that some words can only come after others, and vice versa. This is one of the main differences between these models and CNNS, they take sequences into account as well. The word index dictionary must have all the unique words that we use in our sentences. In this case, the size of the word index, or the total number of unique words we used is simply six. But in real life, there may be hundreds of thousands of words that would need to be indexed (millions if we consider larger models). Thus we first begin by taking our sentences, and indexing each and every word to create unique word vectors. Here’s another example of how a vector would look like in a larger dataset, where there are thousands of words :

\begin{array}{l} S e n t e n c e : S h e o p e n e d t h e d o o r a n d w a s m o r t i f i e d \\ V e c t o r e n c o d i n g : [\begin{array}{ccccccc} 12 & 272 & 3 & 761 & 29 & 122 & 23001 \end{array}] \end{array}

Through the vector we can see that there must be more than 23000 words in that particular word index dictionary. Before we move on, we must not forget that each sentence that we have will be of different length. This can be a problem, as every input vector we use must be of the same length, to form a matrix (vectors of different lengths can’t form a matrix can they?). A simple way around this problem is to apply padding, take the length of the largest vector/sentence (or set one maximum length yourself), and simply add zeros before or after the values in a vector till it reaches the desired length. For instance, if the maximum length is 10 (of the largest sentence, or the one you set), the above vector will be :

\begin{array}{l} P o s t - p a d d i n g : [\begin{array}{cccccccccc} 12 & 272 & 3 & 761 & 29 & 122 & 23001 & 0 & 0 & 0 \end{array}] \\ P r e - p a d d i n g : [\begin{array}{cccccccccc} 0 & 0 & 0 & 12 & 272 & 3 & 761 & 29 & 122 & 23001 \end{array}] \end{array}

The Embedding Layer

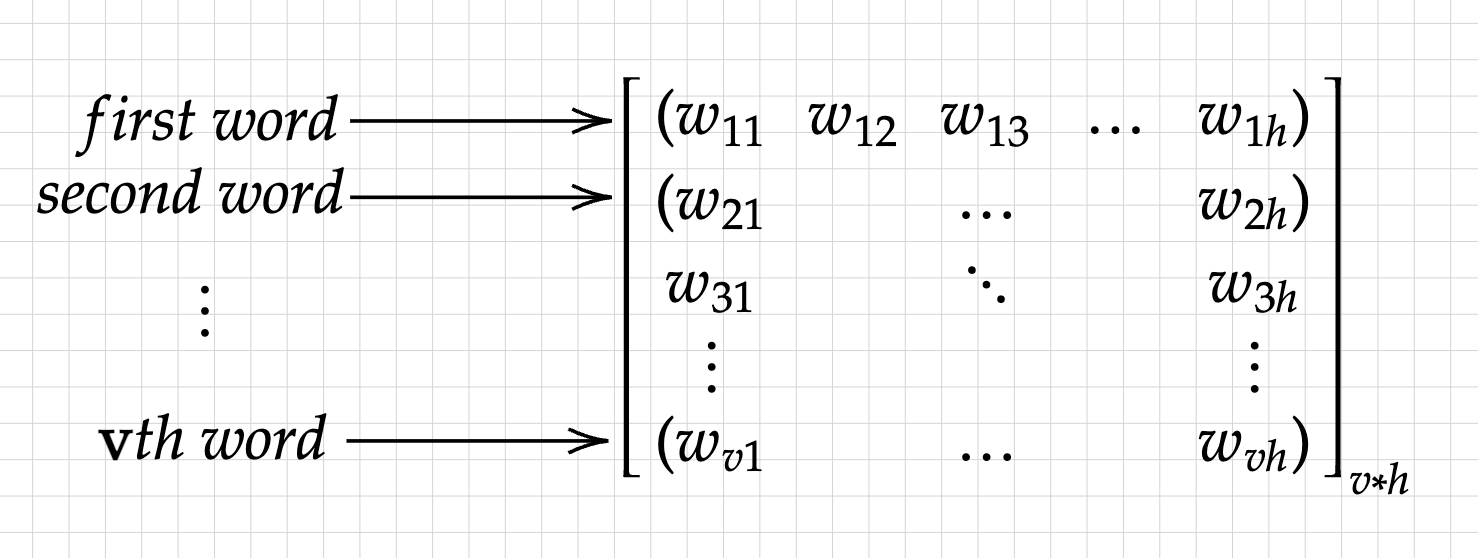
After we get our words vectorized, we simply have to follow the usual procedure of forward propagation, with a slight twist. Let us define a weights matrix (ignoring the bias vector for simplicity). The weight matrix, W₁, will have the following dimenions: v x h, where v is the length of the word index dictionary, or the total number of words we have, and h can be any number we want. The matrix is thus:

𝐖_{1} = {[\begin{array}{ccccc} w_{11} & w_{12} & w_{13} & \dots & w_{1 h} \\ w_{21} \\ w_{31} & ⋱ & ⋮ \\ ⋮ \\ w_{v 1} & \dots & w_{v h} \end{array}]}_{v * h}

This is our weights matrix. Each row in this matrix correspondes to each word, in short, this matrix is a collection of different vectors, each representing a word in our dictionary. At the beginning, they are random. Ounce the learning process starts, the model will tweak and change these weights to better represent the underlying meaning of the word.

In a gist, we provide the model with a vector of sentences, each containing the indexes of the words, the model initiliazes the weights, where each word has a vector of specified dimensions (could be any number of dimenions), and we get the output. But here, we have to apply a sort of shortcut to get to our final product. We only require the rows weights of the word in the sentences, and have no use for the other word weights for that iteration. This is where the indexes in the vector come in handy. We select the rows according to the indexes and get to our output. To achieve this, we can simply use a permutation of a sparse matrix, with dimensions of h * v. For example, suppose we have a bunch of sentences, with 8 words in total. We represent these, words by 1 * h dimensional vectors in the weight matrix, making it 8 * h. Next we simply utilize the indexes in our sentence s, to create a sparse matrix of ones, in order to get out final output of the embedding layer: a matrix of weights representing that particular sentence.

s e n t e n c e v e c t o r = [\begin{array}{ccccc} 3 & 1 & 5 & 7 & 2 \end{array}]

{[\begin{array}{cccccccc} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}]}_{5 * 8} {[\begin{array}{cccc} w_{1,1} & w_{1,2} & \dots & w_{1, h} \\ w_{2,1} \\ w_{3,1} \\ w_{4,1} & ⋱ & ⋮ \\ w_{5,1} \\ w_{6,1} \\ w_{7,1} \\ w_{8,1} & \dots & w_{8, h} \end{array}]}_{8 * h} = {[\begin{array}{ccccc} w_{𝟑,𝟏} & w_{𝟑,𝟐} & w_{𝟑,𝟑} & \dots & w_{3, h} \\ w_{𝟏,𝟏} \\ w_{𝟓,𝟏} & ⋱ & ⋮ \\ w_{𝟕,𝟏} \\ w_{𝟐,𝟏} & \dots & w_{2, h} \end{array}]}_{5 * h}

This is the matrix that will be passed along to the next and final layer.

Forward Propagation

As we get our matrix, as the output from the previous layer, we must do one more thing: average the weight values. As mentioned before, each word will have a vector of certain length assigned to it. To get a good metric, we simply average these vectors, to go from 1 * h dimensions to a scalar, and hence reducing the matrix to a vector again. This particular step isn’t necessary, but since it seems to enhance the quality of my model, I decided to include it here as well. This step is called Global Average Pooling, where we take the average of the values and hence pool together a matrix into a vector.

{[\begin{array}{ccccc} h_{11} & h_{12} & h_{13} & \dots & h_{1 y} \\ h_{21} \\ h_{31} & ⋱ & ⋮ \\ ⋮ \\ h_{x 1} & \dots & h_{x y} \end{array}]}_{x * y} \Rightarrow {[\begin{array}{c} \sum_{i = 0}^{y} h_{1 i} \\ \sum_{i = 0}^{y} h_{2 i} \\ \sum_{i = 0}^{y} h_{3 i} \\ ⋮ \\ \sum_{i = 0}^{y} h_{x i} \end{array}]}_{x * 1}

Proceding further, we pass it onto the next and final layer. This remaining task is very simple: since we need a single number/scalar as our output in order to learn from the true value/sentiment of the statement, we just need to convert the vector into a scalar, i.e, just reduce it again.

{[\begin{array}{c} \sum_{i = 0}^{y} h_{1 i} \\ \sum_{i = 0}^{y} h_{2 i} \\ \sum_{i = 0}^{y} h_{3 i} \\ ⋮ \\ \sum_{i = 0}^{y} h_{x i} \end{array}]}_{x * 1} \Rightarrow [\begin{array}{c} \sum_{j = 0}^{x} \sum_{i = 0}^{y} h_{j i} \end{array}]

With this, we have our initial or the very first “guess” our model has provided at the ground truth, or the actual sentiment of the sentence. But before we move further, we must make it more convinient for the model to learn. Since our targets, or the actual ground truths are -1, 0 and 1, it would be better if our predictions were also between -1 and 1. Hence, as a final layer, we pass it through an activation function, known as Tanh. This function simply takes an input, and squishes it to be between -1 and 1.

\begin{array}{l} T a n h a c t i v a t i o n : \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} \\ O u t p u t : \frac{e^{[\begin{array}{c} \sum_{j = 0}^{x} \sum_{i = 0}^{y} h_{j i} \end{array}]} - e^{- [\begin{array}{c} \sum_{j = 0}^{x} \sum_{i = 0}^{y} h_{j i} \end{array}]}}{e^{[\begin{array}{c} \sum_{j = 0}^{x} \sum_{i = 0}^{y} h_{j i} \end{array}]} + e^{- [\begin{array}{c} \sum_{j = 0}^{x} \sum_{i = 0}^{y} h_{j i} \end{array}]}} \end{array}

With this, we finally have our output. Thus we must proceed further to perform the most important step, stochastic gradient descent or in other words, backpropagation.

Continure Reading
Home