Exploring architectures- RNN

Introduction

In the previous essays, I explored various neural networks architectures purely through math, or from a mathematical perspective (it’s linear algebra anyways). Continuing the trend, in this essay, I will try to work through how a recurrent neural network works from a pure mathematics view, as it provides for the how a network works, as well as the very essential why. These architectures can become very tedious to calculate by hand (as I do), especially with all the matrices and calculus involved, hence I typically only perform single-layer and single-input calculations (as it can be easily extrapolated and duplicated to multiple-layers or multiple-inputs/batches). That being said, before reading this essay, I’d recommend reading my previous essays (Neural Networks, Automatic differentiation and Word embeddings) before going further, and henceforth I am assuming a familiarity with the topics discussed in the previous essays.

Language Models and Recurrent Neural Networks

The attempt to model a computer to mimic human language has been the goal of many scientists and computational linguists since the advent of computer and the desire to achieve artificial intelligence. Our language has one of the most complex underlying statisitcal distribution, and is indeed extremely tough to mimic, even by humans unless they are programmed from a very early age. Various efforts have been made in order to instruct a machine to speak like in throughout the last century. The early language models were our initial attempts before modern networks took over. I will not talk about the intricacies of such langauge models here, but anyone interesed can check out thissite, for some background, about what they are.

Word Embeddings

As I have talked about this topic in the previous essays, I will only go over briefly here. In order to apply the power and potential of neural networks in the case of understanding of langauge, we had to first deal with the shift of the type of input we had: from numerical to language, or words. This is an extremely difficult task, as we cannot just simply index them, for indexing gives no intrinsic meaning to the numbers assigned to the words: if ‘the’ was assigned 1, while ‘building’ was assigned 2, numerically, it makes no sense. That is random assignment, where we randomly assign numbers to words, while overlooking the internal structure that the numbers have (if ‘dragon’ was 3, than ‘the’ + ‘building’ = ‘dragon’). Hence we turned towards word embeddings, where a neural networks chooses a vector to represent a word (through training) and hence tries it’s best to approximate the internal structures between the words, and the relationship they have in numbers. (If represented correctly, ‘king’ - ‘man’ + ‘women’ = ‘Queen’ could be a result), where each word is represented by a vector of n-dimensions. A word can have various aspects and meanings to it, depending on the context, hence if the number of dimensions(n) is large, it can capture more approximations or meaningful representations of the word in the form of the vector.

Recurrent Hidden States

As opposed to our previous attempts at processing the given inputs, in language, we need the previous input’s information as well. The next word or letter cannot be guessed without knowing what came prior to it. When it came to architecturs like CNNs or just single layer neural networks (also called Multi-layered perceptrons), the previous inputs were essentially ‘forgotten’, as all the necessary information from the input was stored inside the gradients being passed backwards through backpropagation, while the next input went through forward propagation, without any context or influence from the previous input. This might work for any other type of problem, but not language. In this case, the next output of our model is dependant not only on the input, but the previous inputs and outputs as well. Hence we introduce another matrix (namely H) which captures information from the input forward. This H is called the hidden state (as opposed to a hidden layer) because it is, well, hidden from us and carries the encodings of the previous input data along with it onto the calculation of the next input or the output.

Forward Propagation

Let X be our matrix of inputs. The rows of X represent the inputs that will be fed into the network, they can be representations of a word or a letter. Let the dimensions be i x d, where there are i inputs, each of d dimensions. In some cases, h can be indivisual character representations or word representations. As per the usual procedure, we first multiply the input matrix by a weight parameter, and add a bias vector to it, but in this case, we want the previous information to persist, and hence we initiate a hidden state H. Our output at any time step will depend upon not only the weight and bias parameters, but also this hidden state which will be used, and it’ll be multiplied by another weight parameter to give our output: the next hidden state, and so on. Let W₁₁ and W₁₂ be weights and B be the bias.

\begin{array}{l} 𝐗 = {[\begin{array}{ccccc} x_{11} & \dots & x_{1 d} \\ x_{21} \\ x_{31} & ⋱ & ⋮ \\ ⋮ \\ x_{i 1} & \dots & x_{i d} \end{array}]}_{i 𝐱 d} 𝐇 = {[\begin{array}{ccccc} h_{11} & \dots & h_{1 d} \\ h_{21} \\ h_{31} & ⋱ & ⋮ \\ ⋮ \\ h_{i 1} & \dots & h_{i h} \end{array}]}_{i 𝐱 h} \\ W_{11} = {[\begin{array}{ccccc} w_{11} & \dots & w_{1 h} \\ w_{21} \\ w_{31} & ⋱ & ⋮ \\ ⋮ \\ w_{d 1} & \dots & w_{d h} \end{array}]}_{d 𝐱 h} W_{12} = {[\begin{array}{ccccc} w_{11} & \dots & w_{1 h} \\ w_{21} \\ w_{31} & ⋱ & ⋮ \\ ⋮ \\ w_{h 1} & \dots & w_{h h} \end{array}]}_{h 𝐱 h} \\ 𝐁 = {[\begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \\ ⋮ \\ b_{h} \end{array}]}_{1 𝐱 h} \end{array}

Note: The hidden state can be initialized as a matrix of zeros. Let Relu (ϕ) be our non-linear activation function. Hence our final equation, which determines the next hidden step would be:

𝐇^{'} = ϕ (𝐗 W_{11} + 𝐇 W_{12} + B)

And finally, using that same hidden state, we get our output by another forward propagation method, with another weight and bias parameter.

𝐎 = 𝐇^{'} W_{21} + B_{2}

In this way we arrive at our final output, whatever it might be (like the next word or the next character to be predicted). The next step would be to simply define a loss function, calculate how much each parameters contributes through the gradients and change the paramters accordingly. We start by defining a loss function, known as the mean squared error (MSE) :

𝐋 = (𝐓 - 𝐎)^{2}

The T variable signifies the correct or the truth value in our dataset (if the input was ‘th’, the truth value would be the next logical letter, ‘e’). Hence, utilising these, we can finally calculate our gradients of the five parameters we have, namely W₁₁, W₁₂, W₂₁, B and B₂. We simply make a computational graph, and trace back the various gradients using automatic differentiation (this). Here is our final equation, only in terms of parameters, input and output values :

𝐋 = (𝐓 - ((ϕ (𝐗 W_{11} + 𝐇 W_{12} + B)) W_{21} + B_{2}))^{2}

The above equation highlights the parameters and the final equation that we get at the end of our recurrent neural network. (This equation is specifically for our one layered network). Next we must find how much each parameter contributes to the loss function, in other words, we have to find these terms :

\frac{δ L}{δ W_{11}}, \frac{δ L}{δ W_{12}}, \frac{δ L}{δ W_{21}}, \frac{δ L}{δ 𝐁}, \frac{δ L}{δ 𝐁_{2}}

In order to calculate the gradients, I chose to work it out by hand (for ease of understanding it myself) and drew up a computational graph, which makes it easier for us humans to calculate the gradients, at least for a small network like this. The graph :

The extra variables are just the intermediate variables that our computers use to easily trace back and calculate multiple gradients. With this, we can easily see the gradients like so:

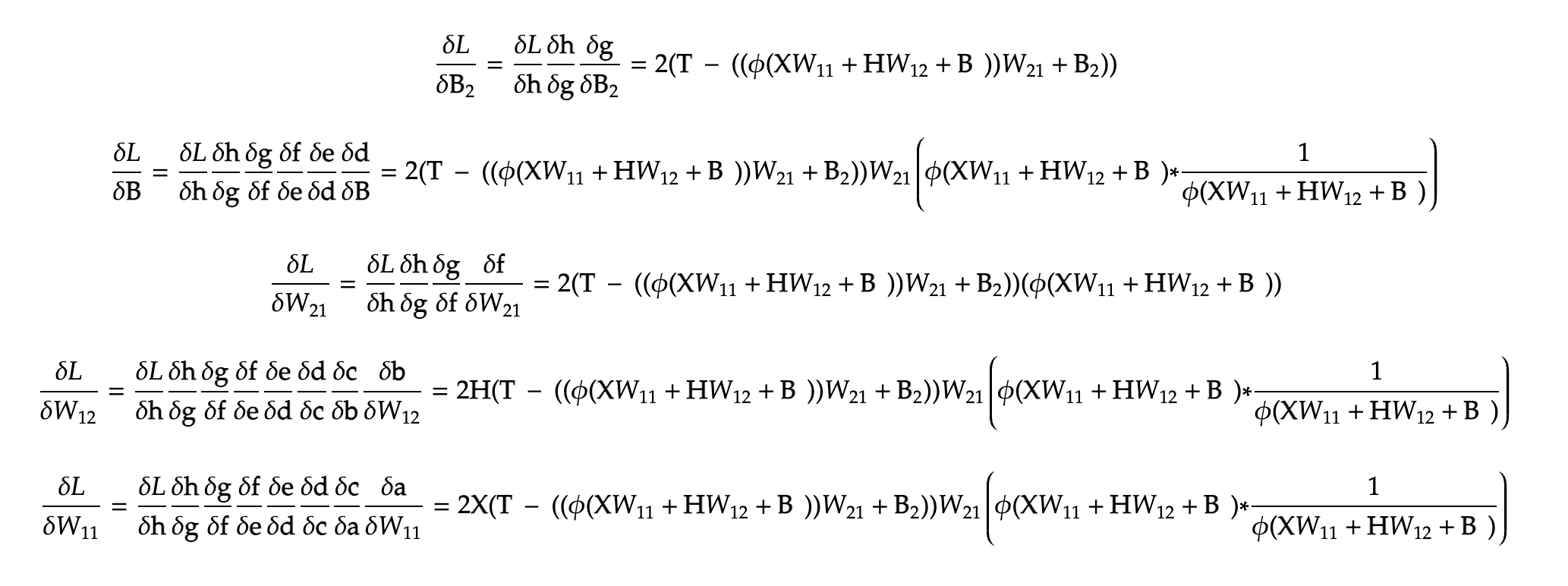
Note: the * symbol is for element-wise matrix multiplication

They are purely in terms of our initial variables, as I removed the intermediates. These now simply need to be subtracted before we restart the process again from forward propagation.

W_{11} - \frac{δ L}{δ W_{11}}, W_{12} - \frac{δ L}{δ W_{12}}, W_{21} - \frac{δ L}{δ W_{21}}, 𝐁 - \frac{δ L}{δ 𝐁}, 𝐁_{2} - \frac{δ L}{δ 𝐁_{2}}

Conclusion

The final recurrent neural network should work fine, but suffers a problem: that of vanishing and exploding gradients. We can see that in the above formulae of gradients, the matrix multiplications can be great, especially due to the recurrent nature of this architecture. This might lead to the gradients accumulating too much, and blowing upto infinity (not quite literally, but at least for us and our computers) or vanishing completely to zero. This might have adverse effects on the training of the networks, and thus needs to be dealt with. One of the methods could be gradient clipping (check out this) or another architecture that builds on RNNs, which will be discussed in the next essay.

Home